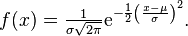Objection:Hasard : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
{{Objection | {{Objection | ||
|objection=Avec le tirage au sort on laisse le hasard décider de nos politiques! | |objection=Avec le tirage au sort on laisse le hasard décider de nos politiques! | ||
| − | |refutation=1) - Si l'assemblée est constitué de suffisamment de membres, elle EST représentative de la population. Chaque cellule du tableau suivant indique | + | |refutation=1) - Si l'assemblée est constitué de suffisamment de membres, elle EST représentative de la population. Chaque cellule du tableau suivant indique la probabilité qu'une décision soit prise par une assemblée tirée au sort : |
http://wiki.gentilsvirus.org/images/9/9f/TableauStatsTaS.jpg | http://wiki.gentilsvirus.org/images/9/9f/TableauStatsTaS.jpg | ||
Version du 15 octobre 2014 à 18:44
| titre court | Hasard |
|---|---|
| objection (titre) | Avec le tirage au sort on laisse le hasard décider de nos politiques! |
| refutation (resume) | 1) - Si l'assemblée est constitué de suffisamment de membres, elle EST représentative de la population. Chaque cellule du tableau suivant indique la probabilité qu'une décision soit prise par une assemblée tirée au sort :
Démonstration : Nous cherchons à quantifier la représentativité d’un échantillon de personnes tirées au sort.
C’est un problème de probabilité binomiale modélisable par une loi normale :
Soit une décision vis-à-vis de laquelle l’opinion publique est favorable à p=51%. Une personne tirée au hasard parmi la population a donc 51% de chance de voter OUI pour cette décision.
Prenons un échantillon n=1000 personnes. On peut calculer l’espérance : dans l’idéal, mu=n.p=510 personnes sont censées voter OUI. On calcule également l’écart-type (qui est un intermédiaire de calcul qui caractérise l’écart entre l’espérance et ce qu’on observera probablement) : sigma=√(n*p*(1-p)) ~ 15.808.
Il suffit alors d’intégrer la fonction densité de probabilité de la loi normale de 500 à 1000 pour obtenir la probabilité pour que le nombre de OUI se situe entre 500 et 1000 ; et que la décision soit donc adoptée :
|
| remarque | |
| urldiscussion | http://sync.in/1EwNoDFK5A |
| Pages liées |