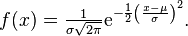Objection:Hasard : Différence entre versions
| (6 révisions intermédiaires par 2 utilisateurs sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
| + | {{Debat|https://www.facebook.com/groups/gentilsvirus/permalink/865010520190176/}} | ||
| + | |||
{{Objection | {{Objection | ||
|objection=Avec le tirage au sort on laisse le hasard décider de nos politiques! | |objection=Avec le tirage au sort on laisse le hasard décider de nos politiques! | ||
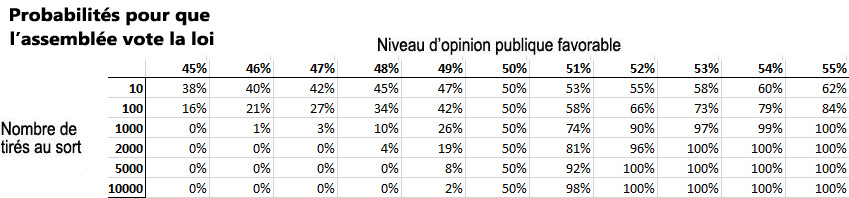
| − | |refutation=1) - | + | |refutation=1) - Si l'assemblée est constitué de suffisamment de membres, elle EST représentative de la population : |
| − | http://wiki.gentilsvirus.org/images/9/9f/ | + | http://wiki.gentilsvirus.org/images/9/9f/TableauTaS.jpg |
| − | Nous cherchons à quantifier la représentativité d’un échantillon de personnes tirées au sort. | + | Démonstration : Nous cherchons à quantifier la représentativité d’un échantillon de personnes tirées au sort. |
C’est un problème de probabilité binomiale modélisable par une loi normale : | C’est un problème de probabilité binomiale modélisable par une loi normale : | ||
Soit une décision vis-à-vis de laquelle l’opinion publique est favorable à p=51%. Une personne tirée au hasard parmi la population a donc 51% de chance de voter OUI pour cette décision. | Soit une décision vis-à-vis de laquelle l’opinion publique est favorable à p=51%. Une personne tirée au hasard parmi la population a donc 51% de chance de voter OUI pour cette décision. | ||
| − | Prenons un échantillon n=1000 personnes. On peut calculer l’espérance : dans l’idéal, mu=n.p=510 personnes sont censées voter OUI. On calcule également l’écart-type (qui est un intermédiaire de calcul qui caractérise l’écart entre l’espérance et ce qu’on observera probablement) : sigma = | + | Prenons un échantillon n=1000 personnes. On peut calculer l’espérance : dans l’idéal, mu=n.p=510 personnes sont censées voter OUI. On calcule également l’écart-type (qui est un intermédiaire de calcul qui caractérise l’écart entre l’espérance et ce qu’on observera probablement) : sigma=√(n*p*(1-p)) ~ 15.808. |
| − | Il suffit alors d’intégrer la fonction densité de probabilité de la loi normale de 500 à 1000 pour obtenir la probabilité pour que le nombre de OUI se situe entre 500 et 1000 ; et que la décision soit donc adoptée | + | Il suffit alors d’intégrer la fonction densité de probabilité de la loi normale de 500 à 1000 pour obtenir la probabilité pour que le nombre de OUI se situe entre 500 et 1000 ; et que la décision soit donc adoptée :<br> |
| − | + | ||
| + | http://upload.wikimedia.org/math/d/7/9/d791e0d4d3e52604fb5d0f974499a9c5.png | ||
| + | <br><br> | ||
| + | On obtient 73.6497%. | ||
<br><br> | <br><br> | ||
2) - Les citoyens sont des humains et ne conçoivent pas leurs idées au hasard.<br><br> | 2) - Les citoyens sont des humains et ne conçoivent pas leurs idées au hasard.<br><br> | ||
| Ligne 19 : | Ligne 23 : | ||
|urldiscussion=http://sync.in/1EwNoDFK5A | |urldiscussion=http://sync.in/1EwNoDFK5A | ||
}} | }} | ||
| + | |||
| + | [[Category:Tirage au Sort]] | ||
Version actuelle en date du 24 octobre 2014 à 10:23
Discussion externe au wiki sur cet article - Discussions internes au wiki sur cet article
| titre court | Hasard |
|---|---|
| objection (titre) | Avec le tirage au sort on laisse le hasard décider de nos politiques! |
| refutation (resume) | 1) - Si l'assemblée est constitué de suffisamment de membres, elle EST représentative de la population :
Démonstration : Nous cherchons à quantifier la représentativité d’un échantillon de personnes tirées au sort.
C’est un problème de probabilité binomiale modélisable par une loi normale :
Soit une décision vis-à-vis de laquelle l’opinion publique est favorable à p=51%. Une personne tirée au hasard parmi la population a donc 51% de chance de voter OUI pour cette décision.
Prenons un échantillon n=1000 personnes. On peut calculer l’espérance : dans l’idéal, mu=n.p=510 personnes sont censées voter OUI. On calcule également l’écart-type (qui est un intermédiaire de calcul qui caractérise l’écart entre l’espérance et ce qu’on observera probablement) : sigma=√(n*p*(1-p)) ~ 15.808.
Il suffit alors d’intégrer la fonction densité de probabilité de la loi normale de 500 à 1000 pour obtenir la probabilité pour que le nombre de OUI se situe entre 500 et 1000 ; et que la décision soit donc adoptée :
|
| remarque | |
| urldiscussion | http://sync.in/1EwNoDFK5A |
| Pages liées |